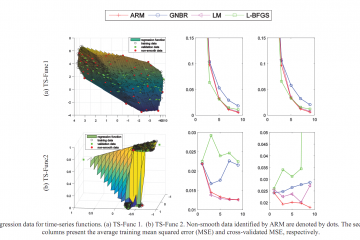
We investigate a method to decide the weight decay parameter values of a deep convolutional neural network that yields a good generalization. To obtain such a CNN in practice, numerical trials with different weight decay values are needed. However, the larger the CNN architecture is, the higher is the computational cost of the trials. To address this problem, we formulates an analytical solution for the decay parameter through a proposed objective function in conjunction with Bayesian probability distributions. For computational efficiency, a novel method to approximate this solution is suggested. Our method uses a small amount of information in the Hessian matrix. Theoretically, the approximate solution is guaranteed by a provable bound and is obtained by a proposed algorithm, where its time complexity is linear in terms of both the depth and width of the CNN. The bound provides a consistent result for the proposed learning scheme. By reducing the computational cost of determining the decay value, the approximation allows for the fast investigation of a deep CNN which yields a small generalization error.

Related publications
1. J Park, S Jo, Bayesian Weight Decay on Bounded Approximation for Learning Deep Convolutional Neural Networks, IEEE T Neural Networks & Learning Systems, 30(9), 2866-2875, 2019. [LINK] [PDF]