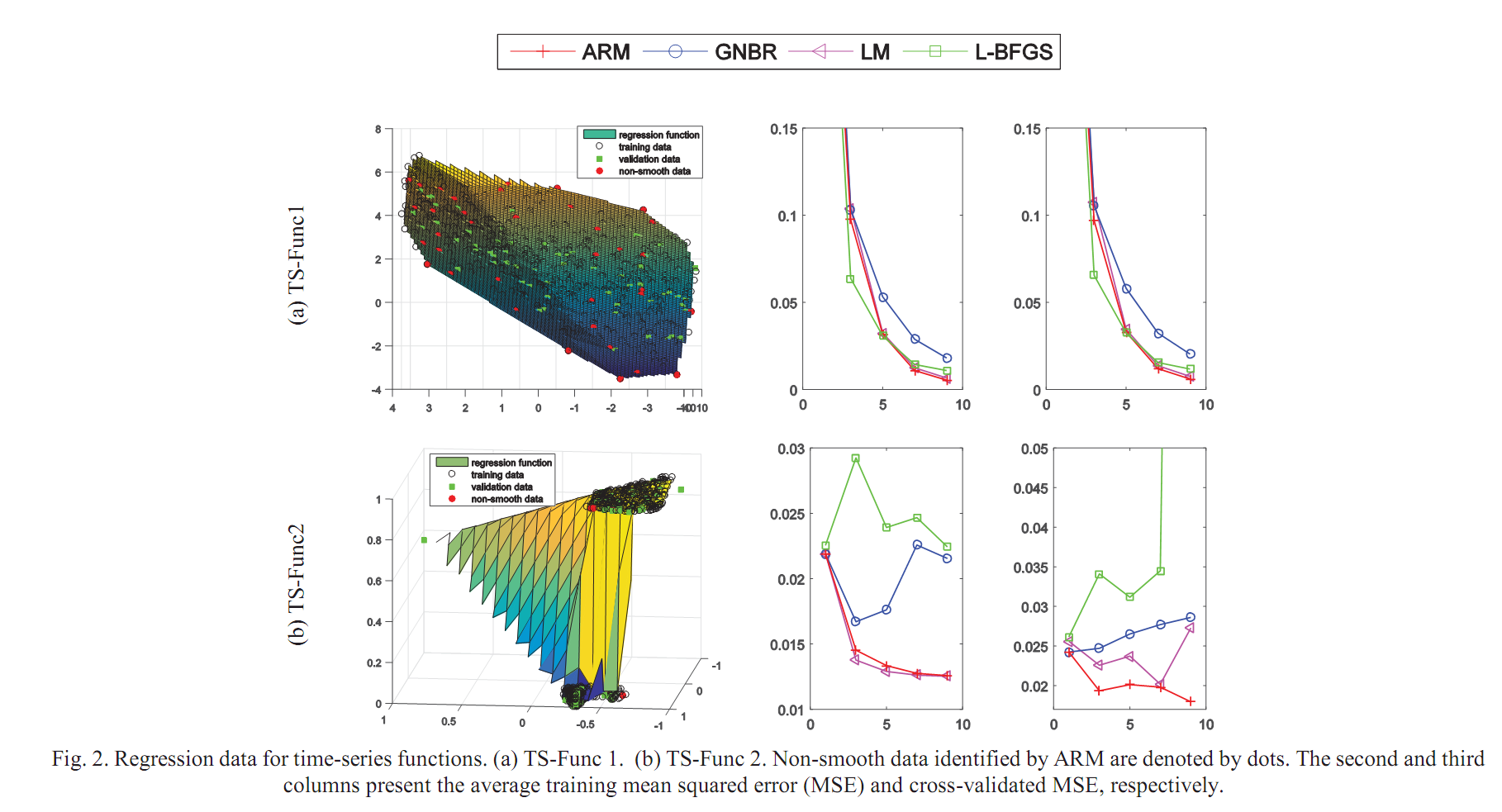
We present a novel regularization method for a multilayer perceptron (MLP) that learns a regression function in the presence of noise regardless of how smooth the function is. Unlike general MLP regularization methods assuming that a regression function is smooth, the proposed regularization method is also valid when a regression function has discontinuities (non-smoothness). Since a true regression function to be learned is unknown, we examine a training set with our Bayesian approach that identifies non-smooth data, analyzing discontinuities in a regression function. The use of a Bayesian probability distribution identifies the non-smooth data. These identified data is used in a proposed objective function to fit an MLP response to the desired regression function regardless of its smoothness and noise. Experimental simulations show that the MLP with our presented training method yields more accurate fits to non-smooth functions than other MLP training methods. Further, we show that the suggested training methodology can be incorporated with deep learning models.